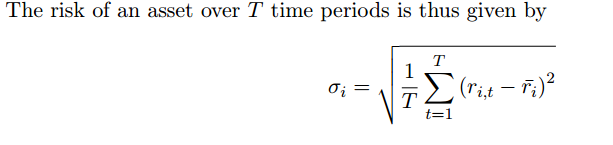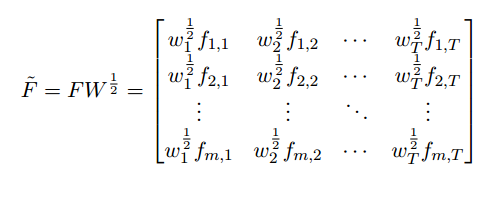Computing sample statistics directly from historical data, however, is fraught with danger. Historical returns are typically noisy; even in the absence of actual data errors, false signals and spurious relationships abound. Two assets may appear closely related when their seemingly-correlated behavior is in fact an artifact of data-mining.
Weak signals and noise aside, when a new asset enters the existing universe, there is no reliable way of calculating its relationships with the other assets, because it does not yet possess a returns history. One could construct various proxies, but such an approach is dubious at best.
Finally, data points totalling no less than the number of assets are required to accurately estimate all the variances and covariances directly. For any realistic number of assets, it is extremely unlikely that sufficient observations exist. Even with a universe of 100 assets, over 1 2 · 100 · (100+ 1) > 5; 000 relationships need to be estimated. For stock markets like the U.S. (over 12,000 assets), this becomes completely infeasible.
A better approach is to first impose some structure on the asset returns by identifying common factors within the market | that is, factors which drive asset returns.
r = Bf + u , B are factor exposures, f are coefficients, u are residuals.
3.1 Least Square Regression solution
4. Residuals are normally-distributed: strengthening the previous assumption to u ∼ N (0; Ω)where Ω = σ2In is not strictly required. Nevertheless, it is a convenient assumption for testing the estimators, to simplify constructing confidence intervals, evaluating hypothesis tests, and so forth.